https://www.acmicpc.net/problem/11659
다음의 문제를 기반으로 누적합과 브루트 포스에 대해 공부하였다
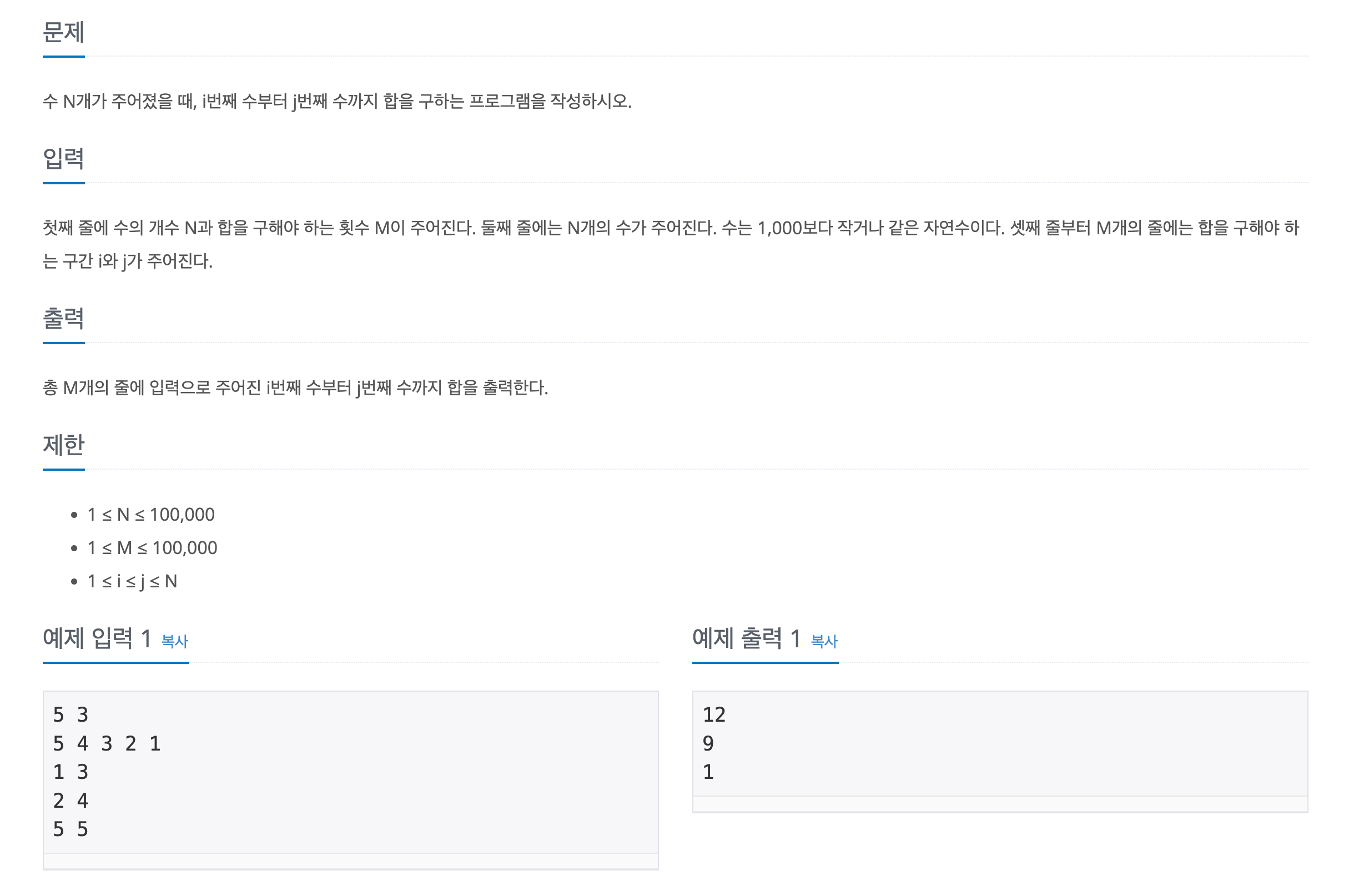
우선 먼저 브루트 포스의 방법으로 해결을 시도하였다
import sys
input = sys.stdin.readline
n,m = map(int,input().split())
s = list(map(int,input().split()))
num = 0
for _ in range(m) :
i,j = map(int,input().split())
for k in range(i-1,j) :
num += s[k]
print(num)
num = 0
직관적으로 계산을 바로 시도 하는 브루트 포스로 해결을 시도하였다
하지만 당연하게도 시간 초과가 발생하였다
https://hcr3066.tistory.com/26
알고리즘 기법[전체 탐색] - 브루트 포스(brute force)
암호학에서의 브루트 포스(brute force attack)가 아닌 알고리즘의 브루트 포스(brute force search)에 관한 것을 작성한다. 브루트 포스(brute force) brute: 무식한, force: 힘 무식한 힘으로 해석할 수 있다. 완
hcr3066.tistory.com
다음의 블로그를 보게되면 모든 경우의 수를 입력하다 보니 시간 복잡도는 O(N*M)으로 총 10억개의 경우의 수가 발생하였고 그에 따라 시간 초과가 발생하는 것은 당연하다
그리하여 누적합으로 재구성 하였다
import sys
input = sys.stdin.readline
n,m = map(int,input().split())
numbers = list(map(int,input().split()))
prefix = [0] * (n+1)
for i in range(1,n+1) :
prefix[i] = prefix[i-1] + numbers[i-1]
for _ in range(m) :
i,j = map(int,input().split())
print(prefix[j] - prefix[i-1])
다음의 방식으로 perfix라는 점화식을 만들어 n만큼의 합을 저장하고(누적합) 이를 꺼내오는 동적계획법으로 재구성 하였다
이렇게 될 경우 시간 복잡도는 O(1)로 계산의 범위가 정해질 경우 1번 실행되므로 시간복잡도가 기하급수적으로 감소하게 된다
'공부일지 > 알고리즘' 카테고리의 다른 글
| [알고리즘] dp와 dfs, bfs (0) | 2025.09.09 |
|---|---|
| [python] 알고리즘 및 자료구조 정리 -2- 필수 라이브러리 및 파이썬의 이점 (4) | 2025.08.08 |
| [python] 알고리즘 및 자료구조 정리 -1- 시간복잡도 (4) | 2025.08.08 |
